-
- HOW MUCH WATTAGE CAN A WIND TURBINE
MAKE?
-
- Any moving object has kinetic energy.
In classical mechanics, its amount E in joules is given by the
equation E=mv2/2,
- where m is the mass in kg, and v is
the speed in m/sec. Air molecules have mass, and when they are
in motion, they
- contain kinetic energy that can be
converted into other forms for practical use.
- When molecules hit a surface of any
object that is allowed to move, their motion is partially transfered
to the moving
- object. Particularly, in wind turbines
the energy is extracted from the air as it moves through the
"swept area" of the
- turbine's blades. During this process
the air turns the aerodynamically designed blades, which transfer
this harvested
- energy into a spinning shaft. The shaft
is connected to a generator's rotor whose motion makes electricity.
HOW MUCH POWER IS IN THE WIND
-
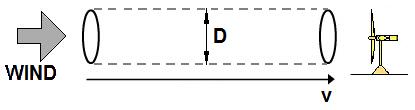
- The wind energy diagram below illustrates
the process of energy transfer. If D is the diameter of the turbine's
blades, they
- intercept the air in the cross-sectional
area A=(D/2)2.
In a time t, the mass of the air that will pass through this
area is m=?xAxvxt, where ? is the density of the air
- (approximately 1.2kg/m3 at sea level).
- By combining the above formulas, we
can calculate the energy of the air that passes through an area
A in a time t:
- E=?xAxv3xt/2
Then power in watts being E per unit time is given by:
- P= ?xAxv3/2
Note that to get the result in watts, all the values in these
formulas have to be expressed in SI units (for non-SI units we
- would need to add some conversion coefficients).
We see that power available in the wind is proportional to the
cube of
- its speed and the size of the turbine's
blades. If for example, the speed doubles, the available watts
increases by a factor of
- eight.
-
- HOW MUCH ELECTRICITY A TURBINE CAN
GENERATE
- The above formula for P represents
the amount of power in the imaginary tube of the air that flows
through the turbine's
- swept area A. However, only a fraction
of this wind power can be actually extracted- there is no way
to harvest all of it. If
- all of air's energy was transfered
to the turbine, the air molecules that hit the blades would have
to come to a complete
- stop. This is impossible since for
continuous operation since the molecules that already hit the
blades need to get out of
- the way to let the air that is behind
them hit the blades. If all the air motion was transferred to
the blades, the air would pile
- up in front of the turbine, and then
the wind would have to blow around the turbine. The fact is,
the air that hits the blades
- must keep some speed to move out of
the way to allow continuous air flow into the turbine. According
to physics, the
- theoretical limit of wind energy that
can be transfered to the shaft is 59.26%. This fact is known
as the Betz Limit. In
- practice, the collection efficiency
of commercially manufactured rotors for home use is typically
25% to 45%. Small
- models for homes tend to have the efficiency
at the lower end of this range.
Example. Suppose you have a micro turbine with blade diameter
1 m (about 3 ft) and efficiency 20%. Let's calculate how
- much electricty it can generate for
your home at the air speed 6 m/sec (which is about 13.4 mph).
- Rotor swept area: A= (D/2)2 = 3.14x(1/2)2
= 0.785 m2
-
- Available power in the wind: Pwind=
?xAxv3/2 = 1.2x0.785x63/2 = 101.7 watt
-
- Then the power that can be extracted
at that speed is: Pturbine=0.20x101.7=20.3 watt.
-
- Note: Betz law says a turbine can only
convert 59% of it's energy into power.
|